Deep double descent explained (4/4)

17/06/2021

Other related works

This series of blog posts was co-written with Marc Lafon. Pdf version is available here as well.

\[ \global\def\Dn{\mathcal{D}_n} \global\def\R{\mathbb{R}} \global\def\LL{\mathcal{L}} \global\def\norm#1{\lVert #1 \rVert} \]

Optimization in the over-parameterized regime

For reasons that are still active research, overparameterization seems beneficial not only in the statistical learning framework, but from an optimization standpoint as well as it facilitates convergence to global minima, in particular with the gradient descent procedures.

The optimization problem can be framed as minimizing a certain loss function \(\LL(w)\) with respect to its parameters \(w \in \mathbb{R}^N\), such as the square loss \(\LL(w) = \frac{1}{2} \sum_{i=1}^n (f(x_i, w) - y_i)^2\) where \(\{(x_i, y_i)\}_{i=1}^{n}\) is our given training dataset and \(f : (\mathbb{R}^d \times \mathbb{R}^N) \rightarrow \mathbb{R}\) is our model.

Exercise 2. Assume that \(\ell: \mathcal{Y} \rightarrow \mathbb{R}\) is convex and \(f : \mathcal{X} \rightarrow \mathcal{Y}\) is linear. Show that \(\ell \circ f\) is convex.

When \(f\) is non-linear however (which is habitually the case in deep learning) the landscape of the loss function is generally non-convex. Therefore, first order methods such as GD or SGD are likely to converge and get trapped in spurious local minima, depending on the initialization. Yet, in the over-parameterized regime where there are multiple global minima interpolating almost perfectly the data, it seems that SGD has no problem converging to these solutions, despite the highly non-convex setting. Recent works are trying to explain this phenomenon.

For instance, Oymak & Soltanolkotabi (2020)¹ shows that, for one-hidden layer neural networks that (1) have smooth activation functions, (2) are over-parameterized, i.e. \(N \geq C n^2\) where C depends on the distribution of the data and (3) are initialized with i.i.d. \(\mathcal{N}(0,1)\) entries, then with high probability GD converges quickly to a global optimum. Similar results also hold for ReLU activation functions and for SGD.

In Liu et al. (2020)², the authors show that sufficiently over-parameterized systems, including wide neural networks, generally satisfy a condition that allows gradient descent to converge efficiently, for a broad class of problems. They use the PL-condition (from Polyak and Lojasiewicz ³) which does not require convexity but is sufficient for efficient minimization by GD. One key point is that the loss function \(\LL(w)\) is generally non-convex in the neighborhood of minimizers. Due to the over-parameterization, the Hessian matrices \(\nabla^2 \LL(w)\) are positive semi-definite but not positive definite in these neighborhoods, which is incompatible with convexity for non-linear sets of solutions. This is in contrast to the under-parameterized landscape which generally has multiple isolated local minima with positive definite Hessian matrices. Figure below illustrates this.

Left : Loss landscape of under-parameterized models, locally convex at local minima. Right : Loss landscape of over-parameterized models, incompatible with local convexity. Taken from Liu et al. (2020)

In addition to better convergence guarantees, over-parameterization can even accelerate optimization. By working with linear neural networks (hence fixed expressiveness), Arora et al. (2018)⁴ finds that increasing depth has an implicit effect on gradient descent, combining certain forms of momentum and adaptive learning rates (two well-known tools in the field of optimization). They observe the acceleration for non-linear networks as well (replacing weight matrices by a product of matrices, for fixed expressiveness), and even when using explicit acceleration methods such as Adam.

Neural networks as a physical system : the jamming transition

In order to study the loss landscape, Spigler et al. (2018)⁵ make an analogy between neural networks and complex physical systems with non-convex energy landscape, called glassy systems. Indeed, the loss function can be interpreted as the potential energy of the system \(f\), with a large number of parameters \(N\) (degrees of freedom). By considering the hinge loss, the minimization of \(\LL(w;\Dn)\) actually amounts to a constraint-classification problem (with \(n\) constraints, \(N\) continuous degrees of freedom), already studied in physics.

Using this analogy, they show that the behavior of deep networks near the interpolation point is similar to the behavior of some granular systems, that undergo a critical jamming transition when their density increases such that they are forced to be in contact one another. In the under-parameterized regime, not all the training examples can be classified correctly, which leads to unsatisfied constraints. But in the over-parameterized regime, there is no stable local minima : the network reaches a global minima zero training loss.

As illustrated in figure below, the authors are able to quantify the location of the jamming transition in the \((n, N)\) plane (considering \(N\) as the effective number of parameters of the network). Considering a fully-connected network with arbitrary depth, ReLU activation functions and a dataset of size \(n\), they give a linear upper bound on the critical number of parameters \(N^*\) characterizing the jamming transition : \(N^* \leq \frac{1}{C_0} n\) where \(C_0\) is a constant. In their experiments, it seems that the bound is tight for random data but that \(N^*\) increases sub-linearly with \(n\) for structured data (e.g. MNIST).

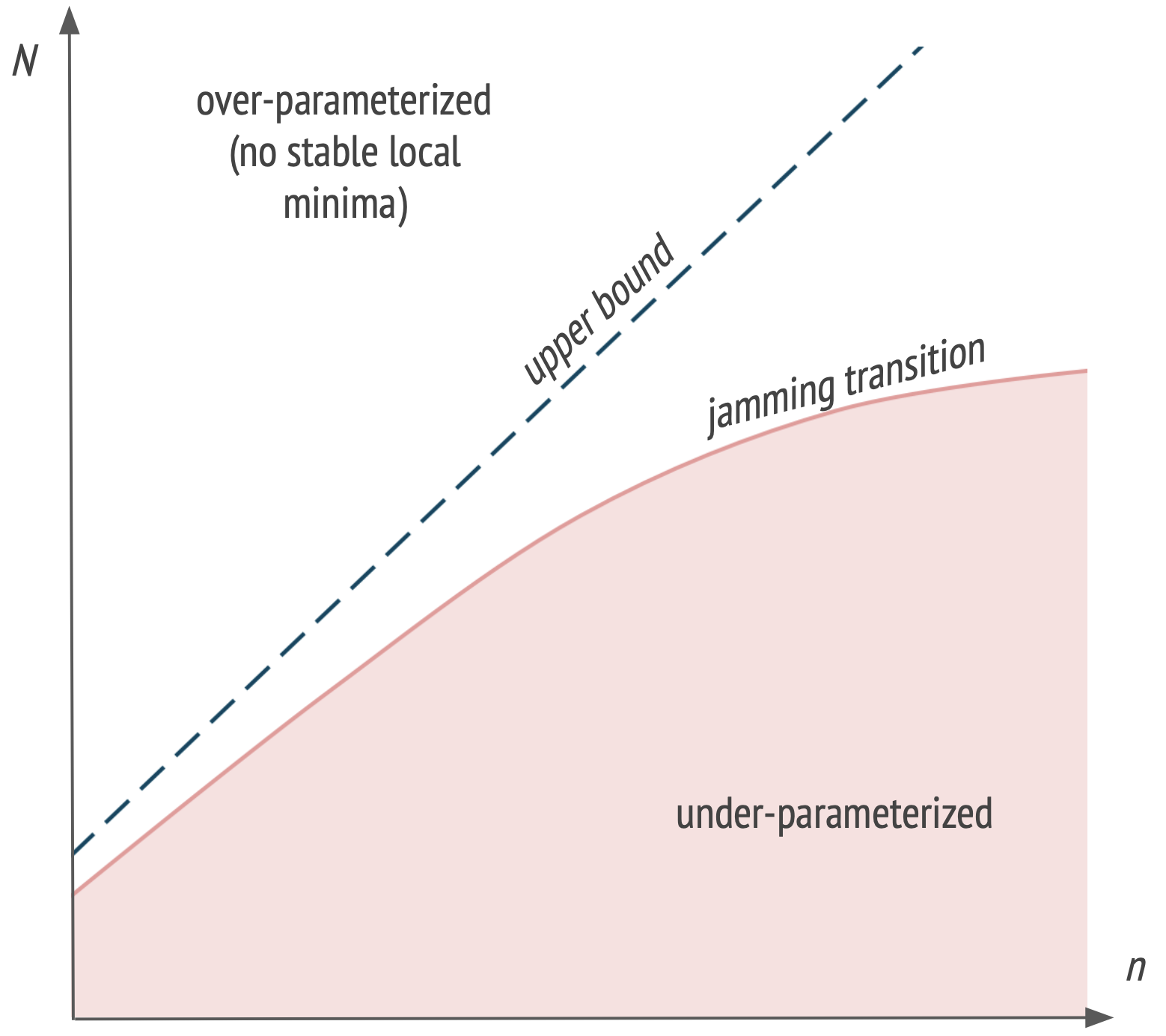
\(N\) : degrees of freedom, \(n\) : training examples. Inspired from Spigler et al. (2018)

Similarly to other works, they observe a peak in test error at the jamming transition. In Geiger et al. (2020)⁶, using the same setting of fixed-depth fully-connected networks, they argue that this may be due to \(\norm{f}\) diverging near the interpolation point \(N=N^*\). Interestingly, they also observe that near-optimal generalization can be obtained using an ensemble average of networks with \(N\) slightly beyond \(N^*\).

Conclusion

From a statistical learning point of view, deep learning is a challenging setting to study and some recent empirical successes are not yet well understood. The double descent phenomenon, arising from well-chosen inductive biases in the over-parameterized regime, has been studied in linear settings ⁷ and observed with deep networks ⁸.

In addition to the references presented in this post, other lines of work seem promising. Notably, ^{9 10 11 12} are working towards a better understanding of the implicit bias induced by optimization algorithms. Finally, we refer the reader to subsequent works of Belkin et al. such as ¹³, that finds multiple descent curves with an arbitrary number of peaks, due to the interaction between the properties of the data and the inductive biases of learning algorithms.